Optique des ondes guidées

À connaître

équations de Maxwell
conditions aux limites du guide : continuité et continuité de la dérivée
approximation de guidage faible $\Delta = \frac{n_1-n_2}{n_1} \simeq 0$
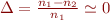
résolution graphique pour les modes propageants
notations normalisées
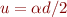- $u = \alpha d/2$ constante de propagation transverse réduite
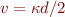- $v = \kappa d/2$ coefficient d'extinction réduit
- $V = k_0 d \sqrt{n_1^2-n_2^2}$ fréquence réduite
  - $u^2 + v^2 = (V/2)^2$
condition de guidage $k_0^2n_2^2 < \beta < k_0^2n_1^2$

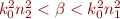
Les équations de Maxwell en tenant compte des invariances donnent les résultats TE et TM. Les ondes guidées sont une combinaison de ces solutions (ne sont pas TEM).

Modes guidés TE

Si la condition de guidage est satisfaite, les équations de propagation s'écrivent :

$\text{pour } |x| < d/2, \quad \frac{d^2E_y}{dx^2}+\alpha^2E_y=0, \quad \text{avec } \alpha^2 = k_0^2n_1^2-\beta^2 > 0$

$\text{pour } |x| > d/2, \quad \frac{d^2E_y}{dx^2}-\kappa^2E_y=0, \quad \text{avec } \kappa^2 = \beta^2 - k_0^2n_2^2 > 0$

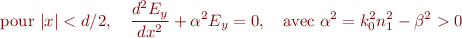
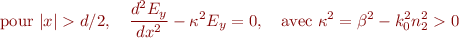
Les solutions physiques sont :

$\text{pour } |x|<d/2 \quad E_y(x)=A\cos\alpha x + B\sin\alpha x$

$\text{pour } x>d/2 \quad E_y(x) = D\exp -\kappa x$

$\text{pour } x<-d/2 \quad E_y(x) = C\exp \kappa x$

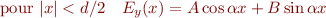
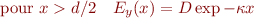
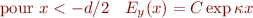
Solutions symétriques [antisymétriques]

Pour un guide d'onde plan, les solutions symétriques [antisymétriques] ont des solutions si $u\tan u=\sqrt{(V/2)^2-u^2}$ , [ $-u\cot u=\sqrt{(V/2)^2-u^2}$ ]

Approximation de guidage faible

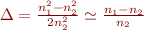L'approximation de guidage faible peut être faite quand les indices des deux milieux mis en jeu sont proches. Le paramètre de guidage $\Delta$ peut être approché en $\Delta = \frac{n_1^2 - n_2^2}{2n_2^2} \simeq \frac{n_1-n_2}{n_2}$ . De plus, le nombre de modes doit être faible, donc la fréquence réduite aussi.

Dans cette approximation, les modes sont polarisés linéairement et TEM.