Menu de WikiSupop
Outils pour utilisateurs
Panneau latéral
fiches:polarisation
Table des matières
Polarisation
Formalisme à savoir manipuler
- vecteur de Jones
- sphère de Poincaré
- matrice de Jones
- ellipsoïdes des indices
- surface des vitesses radiales
- surface des indices
- matrice de cohérence (de covariance)
- vecteur de Stockes
- matrice de Mueller
- ellipticité et azimut
Définitions
Vecteur de Jones = représentation complexe du champ électrique
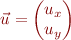
Matrice de cohérence
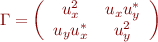
Vecteur de Stockes
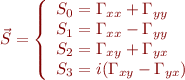
Matrice de Mueller (où J est la matrice de Jones)
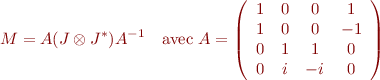
Composants à connaître
- lame demi-onde
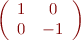
- lame quart d'onde
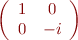
- polariseur rectiligne
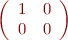
- déphaseur
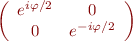
- rotateur
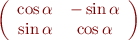
- cube séparateur de polarisation
- cellule à cristaux liquides
- milieu uniaxe/biaxe
fiches/polarisation.txt · Dernière modification: 2016/11/09 15:53 (modification externe)
Outils de la page
Sauf mention contraire, le contenu de ce wiki est placé sous les termes de la licence suivante : CC Attribution-Share Alike 3.0 Unported

